If the distance between center to chord is 12 cm and the length of the chord is 10 cm, then the diameter of the circle is
A26 cm
B14 cm
C13 cm
D30 cm
A26 cm
B14 cm
C13 cm
D30 cm
Related Questions:
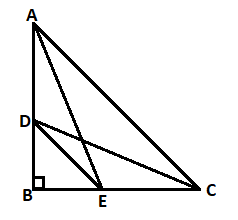
In the figure given below, B is a right angle. If DB = 6 cm, DC = 12 cm and AB = 14 cm, then find the length of AC.